Bayes
このページではベイズ最適化について簡単に解説しています。
三井情報株式会社と共同でベイズ最適化のアプリを開発しました!
無料で使える試作版アプリはこちら(https://mki-bayesopt-v2.mkilabs.io/mitools)
マテリアルの探索をする研究現場では、マテリアルを構成する元素の多様化および温度や圧力といった合成条件の精緻化によって、それらの組み合わせが急拡大し、効率的なマテリアル探索が求められています。合成条件を効率よく最適化するための手法として注目されているのがベイズ最適化です。今回開発した試作版アプリを用いれば、プログラミングや機械学習の知識がなくても、Webブラウザ上でベイズ最適化を無料で実行することができます。合成パラメータは一次元及び二次元の場合にのみ対応しています。ツール画面のイメージはこちらです。
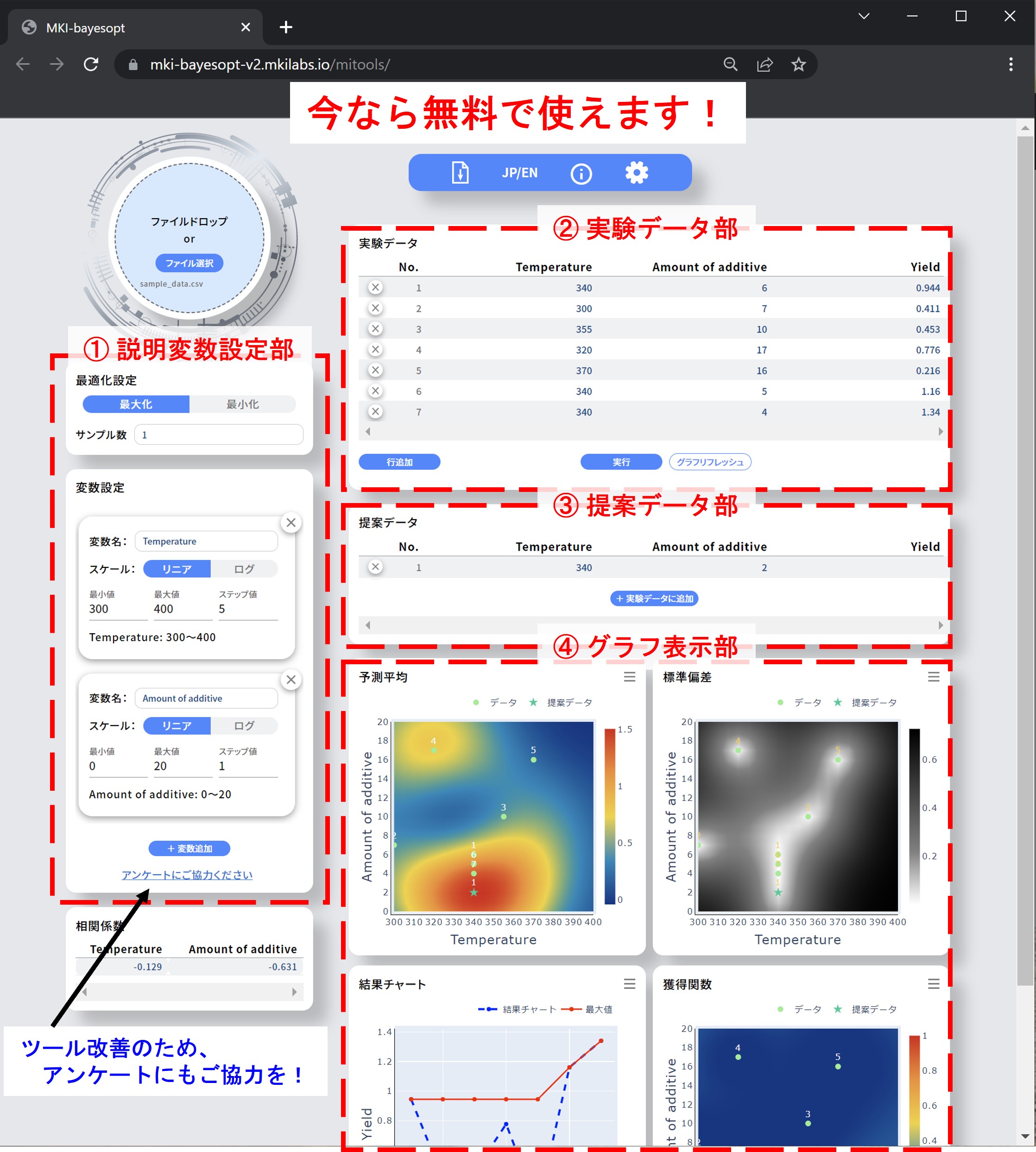
皆様のご意見を踏まえて、ツールの改良を行っていきたいと考えておりますので、アンケートにもご協力いただけますと幸いです。ガウス過程回帰やカーネル・獲得関数についてなど、ベイズ最適化の詳細についてはこの↓で解説しておりますので、合わせてご参照ください。(文責: 中山)
ガウス過程回帰について
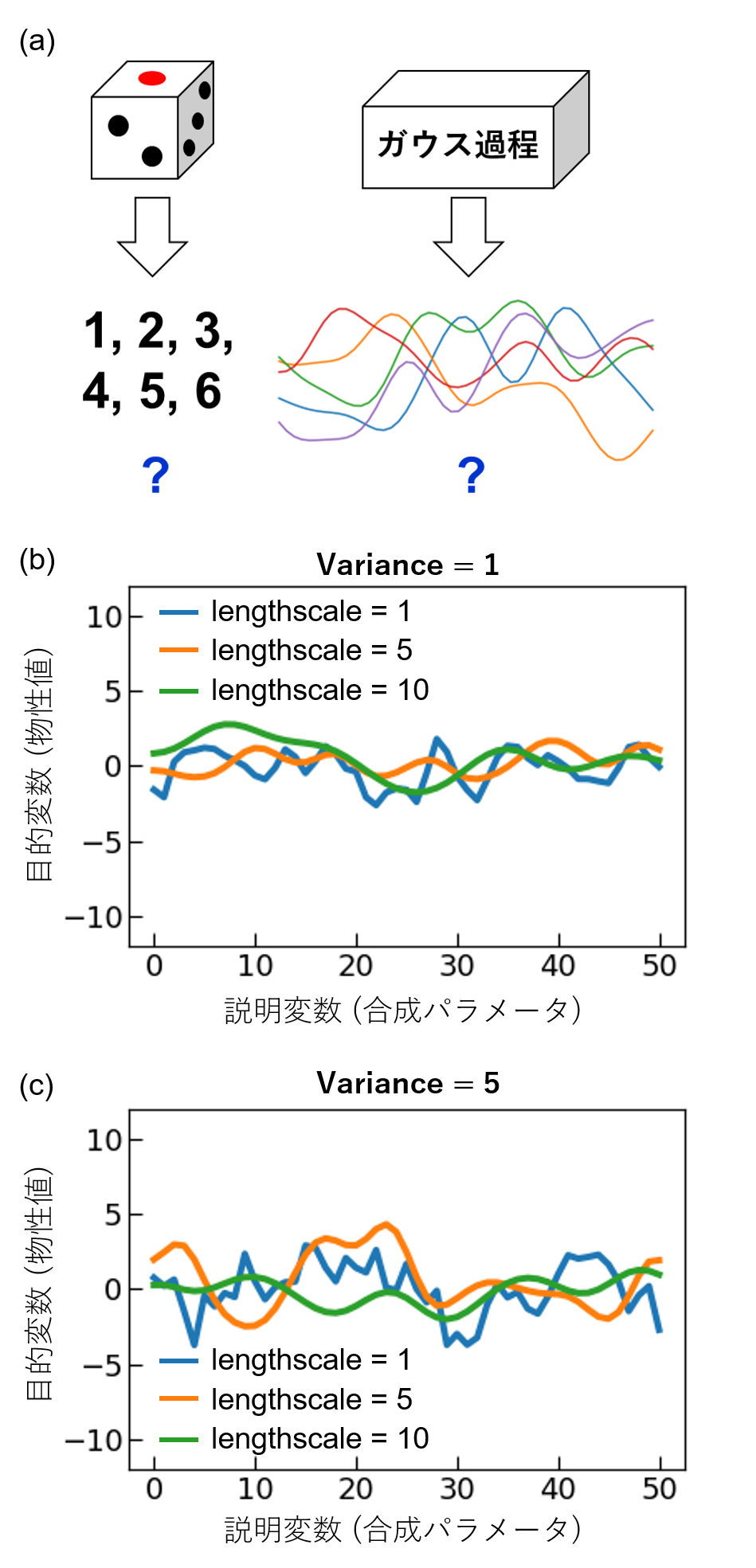
ベイズ最適化では、ガウス過程回帰などにより物性値の予測モデルを作成する。ここで、ガウス過程とは「滑らかさの似た関数f(x)がランダムにポンと出てくるような箱」のようなものだと思ってもらうと良い(図(a))[1]。これはサイコロが、「1, 2, 3, 4, 5, 6の自然数がポンと出てくる箱」と考えるのと同じである。生成する関数の滑らかさはカーネル関数とそのハイパーパラメータによって制御することができる(図(b, c))。理想的なサイコロの場合、それぞれの目が出る確率は1/6であるが、イカサマ用サイコロのように重心が偏ると特定の目が出る確率が上がる。ガウス過程の場合においても、既知のデータがある場合、それに合わせた尤もらしい関数が生成される確率が高くなる。合成条件(説明変数)xにおける目的変数(物性値)は、確率分布(通常は正規分布)p(y│x)の形で表すことができる。事前情報が何もない場合、目的変数の事前分布として一様分布を想定することが多い。この事前分布に実験データが追加されると、更新された事後分布が得られる。すると、事後分布からデータに合わせた尤もらしい関数がランダムに生成されるようになる。確率分布p(y│x)の平均値から物性値の予測、つまり、予測曲線が得られ、確率分布の標準偏差(分散)が予測の不確かさを表す。この時の標準偏差を信頼区間と呼ぶ。(文責: 中山)
[1] 持橋大地、大羽成征、「ガウス過程と機械学習」、講談社、2019.
カーネル関数について
ガウス過程回帰で予測モデル(予測曲線と信頼区間)を得る際に重要となるのがカーネル関数である。大まかにいえば、カーネル関数の役割は、サンプルの類似度を評価するためのものである[1]。材料科学者の直感として、似たような合成条件で作製したサンプルは似たような物性値を示すと考えることができる。例えば、300℃で合成したサンプルの物性値が分かっている場合、合成温度が320℃の場合の実験を行わずとも、その物性値は300℃の結果にある程度近いと予想するだろう。また、合成温度が300℃から離れるにつれて、より異なった物性値を示すと予想できる。この合成条件の”近さ”という人間の直観的な考えを、数学的に表現するための関数がカーネル関数である。予測曲線や信頼区間の形状はカーネル関数によって変化するため、カーネル関数の設定・チューニングは予測モデルを構築する際に重要な役割を果たす。カーネル関数のチューニングに用いるパラメータをハイパーパラメータと呼ぶ。予測曲線や信頼区間の形状はカーネル関数によって変化するため、カーネル関数の設定は予測モデルを構築する際に重要な役割を果たす。ガウス過程回帰で一般的に使用されているカーネル関数がRadial
Basis Function (RBF) カーネルであり、式(1)のように与えられる[2]。
\begin{equation}
k(x,x^{\prime}) = v \times \exp(-\frac{(x-x^{\prime})^{2}}{2l^{2}})
\end{equation}
ここで、x,x^'は説明変数(合成パラメータ)で、lとvがそれぞれlengthscaleとvarianceというハイパーパラメータである。
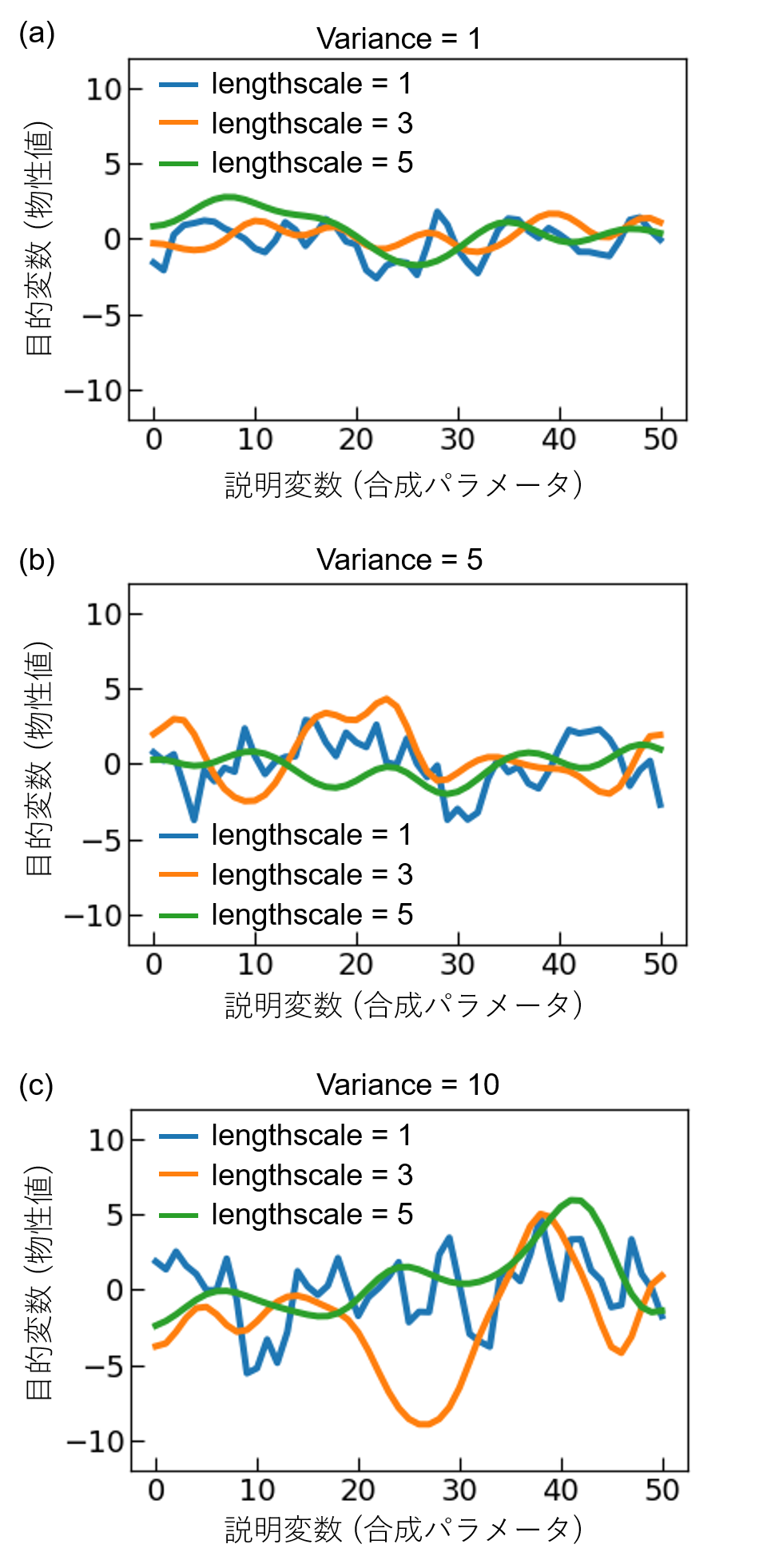
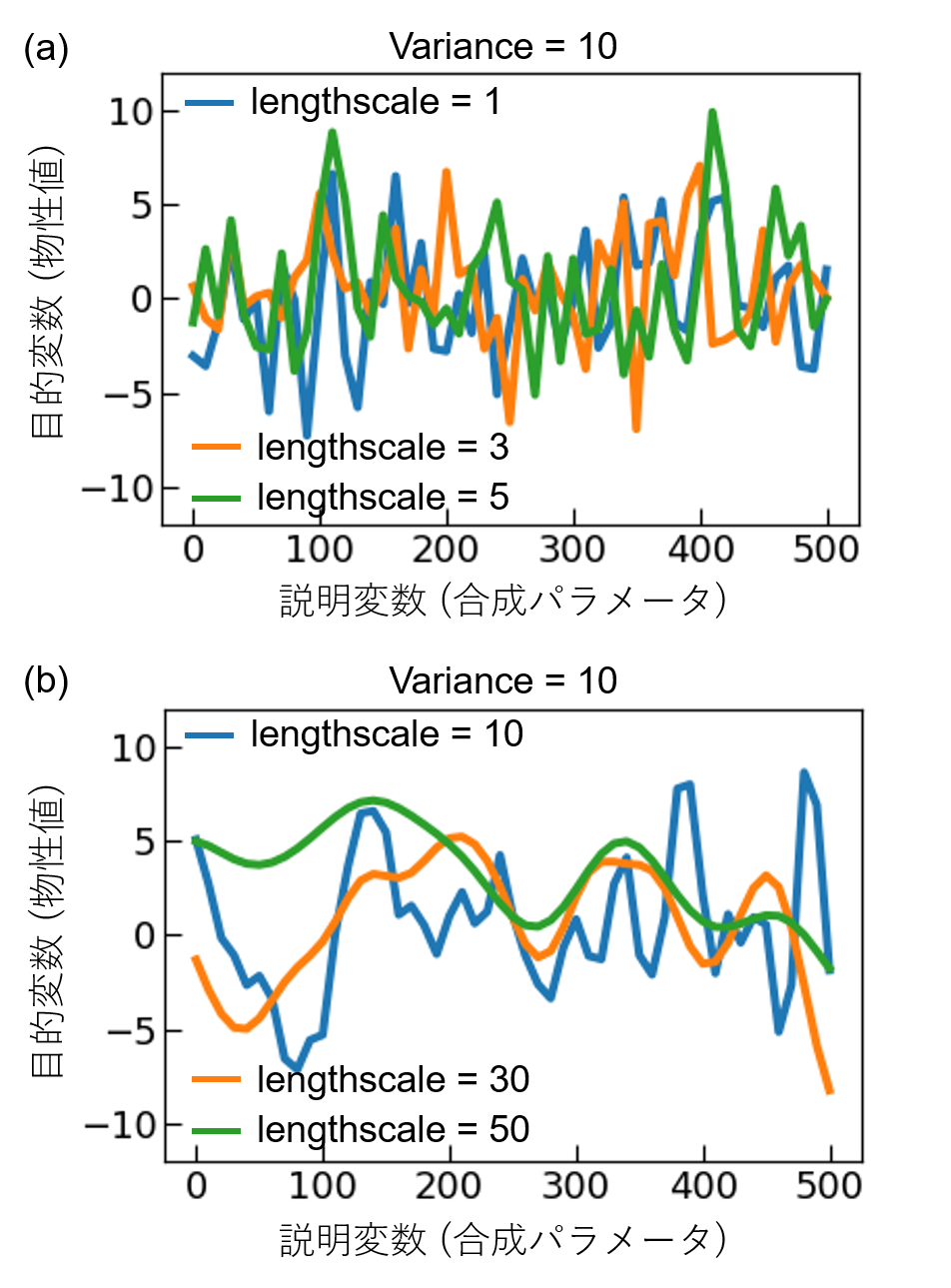
lengthscaleの役割についてまず考える。図1にRBFカーネルを用いてガウス過程により関数を生成した結果を示す。lengthscaleの値が大きくなると、説明変数(合成パラメータ)の変化に対して、目的変数(物性値)がなめらかに変化していることが分かる。なお、合成パラメータが複数ある場合、合成パラメータの変化が指数関数的な場合(例えば圧力など)の場合、lengthscaleの設定には注意が必要である。図1(c)と図2を比較するとわかるように、説明変数のスケールが異なる場合、同じlengthscaleの値を用いたとしても、関数の滑らかさは異なる。そのため、筆者はこのような場合、複数の合成パラメータを全て同じ範囲のグリッドに変換してガウス過程回帰を行っている。例えば、温度Tと圧力Pの二種類の合成パラメータを用いており、それぞれの範囲が200–1200℃、101–10−4
Paの場合を考える。ここで、T=x_1×20+200、P=〖10〗^(1-x_2/10)として、温度T、圧力Pをx1, x2に変換すれば、どちらも0, 1, 2, ...,
50という51点のグリッドとなる。
一方、varianceの値が大きいと、目的変数(物性値)の変化のスケールが大きくなる(図1)。研究者の事前知識として、測定予定の物性値のスケール感が分かる場合はそれを踏まえてvarianceの初期値を設定すると良いが、そうでない場合には実験データの規格化を行うべきだろう。
ガウス過程回帰を扱うGPy[3]というPythonのライブラリでは、lengthscaleとvarianceといったハイパーパラメータを勾配法によって最適化することが可能である。しかし、勾配法によって得られる解は、一般に真の大域的最適解ではなく局所解である。実験データの関係を説明するのに適した予測モデルを得るためには,lengthscaleとvarianceの初期値を適切に与えることが必要である。特に、ベイズ最適化とロボットを組み合わせた自律的な材料合成を行う場合、ループの途中で人間が介在し、ハイパーパラメータを調整しなければならない状況は好ましいとは言えない。したがって、自律実験の最初に適切なハイパーパラメータを選択することが重要となるだろう。(文責:
中山)
[1] 金子弘昌, “Pythonで学ぶ実験計画法入門”, 講談社, 2021.
[2] C. E. Rasmussen and K. I. Williams, “Gaussian Process for Machine Learning”, MIT Press,
2006.
[3] GPy. GPy: A Gaussian process framework in python. http://github.com/SheffieldML/GPy
(2012).
獲得関数について
獲得関数は次の合成条件を決定するために用いる。ベイズ最適化を用いた材
料開発の狙いは少ない実験回数で最大(最小)の物性値を示す材料を得ることに ある。そして、獲得関数の役割は、ガウス過程回帰などによって得られた予測曲
線と信頼区間を踏まえて、大域的最大(最小)値が得られそうな合成条件を示すこ とである。大域的最大値となる合成条件を発見するための戦略を考えてみると、
良い結果が得られる可能性が高いところを探すか、不確実性の高いところで一 発逆転を狙うかという二種類の戦略が考えられる。既に良い結果が得られてい
るところばかりを探すと局所解に陥りやすくなってしまう一方で、不確実性の 高いところばかりを探していると、既知のデータの情報を活かせない。予測値の
大きい合成条件を探す”活用(exploitation)”と標準偏差の大きい合成条件を探す”
探索(exploration)”という二つの戦略のバランスをとることが重要である。
代表的な獲得関数として、Upper Confidence Bound (UCB)と Expected Improvement(EI)の二種類がある[1],[2]。UCB
は以下の式(2)で定義される。
\begin{equation}
\mbox{UCB}(𝑥) = 𝐸(𝑥) + 𝜅 × σ(𝑥)
\end{equation}
ここで,E は予測平均,σ は標準偏差,κ は UCB のハイパーパラメータである。 κ が小さくなるほど、予測値の影響が大きくなり“活用”重視となり、κ が大きく
なるほど、標準偏差の影響が大きくなるので、”探索”重視となる。UCB の利点 はハイパーパラメータ κ により、”探索”と”活用”のバランスを直観的に制御でき
る点にある。
一方、EI は既存のデータにおける目的変数の最大値(𝑓 (𝑥))の更新幅の期待値を関数にとり、以下の式(3)で定義される。
\begin{equation}
\mbox{EI}(x)=(f_{\mbox{max}}(x)-E(x)-ξ)Φ(Z)+σ(x)ϕ(Z)
\end{equation}
ここで、Φ(𝑍)は正規分布の累積分布関数、 𝜙(𝑍)は正規分布の確率密度関数であり、𝑍 = (𝑓 (𝑥) − 𝐸(𝑥) − 𝜉)/𝜎(𝑥)である。ξ は EI
のハイパーパラメータであり、ξ が大きくなるほど、より”探索”重視となる。EI は Probability of Improvement
(PI)という獲得関数の発展形だと捉えることもできる。PI は既存のサンプルにおける目的変数の最大値より大きくなる確率として定義される。定義上、PI
は改善量がどれだけ微小であっても、最大値の改善確率が高ければ、その条件を次の 合成条件として提案してしまう。そのため、局所解に陥る可能性がある。一方、 EI
では最大値の更新幅の期待値として定義されるため、最大値の改善確率が高くとも、改善量が少ない条件は提案されづらくなる。(文責: 中山)
[1] D. R. Jones M. Schonlau, W. J. Welch, “Efficient global
optimization of expensive black-box functions.” Journal of Global optimization. 13, 455-492
(1998).
[2] E. Brochu, V. M. Cora, N. A. de Freitas, “Tutorial on Bayesian Optimization of Expensive
Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement
Learning.” arXiv:1012.2599 (2010).


